How to Subtract Binary Numbers Using Complements

Binary subtraction includes subtracting two binary numbers (0 and 1). It is identical to the fundamental arithmetic subtraction of decimal numbers usually done in basic Math. Only the integers 0 and 1 are used in binary numbers. Because just 0 and 1 are involved, we may need to remove 0 from 1 on some occasions. The concept of borrowing is used in such situations from the next higher-order digit. Borrowing in binary subtraction is the same as in arithmetic subtraction. The binary subtraction rules are:

0 – 0= 0

1 – 0 = 1

1 – 1 = 0

0 – 1 = 1 (Borrow 1)

Example: Subtract 101 from 1010.

Solution: The subtraction of binary numbers 101 and 1010 will be as follows:

$\frac{\begin{array}{r} 1010 \\ - 110 \end{array}}{0101}$

The difference of numbers 101 and 1010 is 0101.

In order to learn Binary Subtraction, we will use the example: 1010 – 101.

$\frac{\begin{array}{r} 1010 \\ - 101 \end{array}}{}$

Step 1: Take the 1's column and subtract it, (0 – 1), yielding 1 as per the binary subtraction condition with a borrow of 1 from the 10's position.

Step 2: The value 1 in the 10's column is changed to the value 0 after borrowing 1 from the 10's column.

1 Borrow

$\frac{\begin{array}{r} 1010 \\ - 101 \end{array}}{1}$

Step 3: Subtract the value in the tenth place, resulting in (0 – 0) = 0.

1 Borrow

$\frac{\begin{array}{r} 1010 \\ - 101 \end{array}}{01}$

Step 4: Subtract the values in the hundredth place. Take 1 from the 1000th position (0 – 1) = 1.

1 1 Borrow

$\frac{\begin{array}{r} 1010 \\ - 101 \end{array}}{0101}$

When we compare the binary subtraction resulting value to the decimal value, we should get the same result. The decimal number 10 is equal to the binary value 1010, while the binary value 101 is equal to 5.

So, 10 – 5 = 5

As a result, the binary number 0101 equals the decimal number 5.

Binary Subtraction Using 1's Complement

1's complement of a number is obtained by interchanging every 0 to 1 and every 1 to 0 in a binary number. For instance, the 1's complement of the binary number 110₂ is 001₂.

The positive sign is represented by the number 0.
The negative sign is represented by number one

Procedure for Binary Subtraction by 1's Complement

The steps to perform binary subtraction using 1's complement are as follows:

Write the subtrahend's 1's complement.
Then, using the minuend, subtract the 1's complement subtrahend.
If there is a carryover in the result, add it in the least significant bit.
If there is no carryover, take the resultant's 1's complement, which is negative.

Example: Subtract (110101)₂ – (100101)₂

Solution: The binary subtraction of (110101)₂ – (100101)₂ will be performed as

(1 1 0 1 0 1)2 = 5310
(1 0 0 1 0 1)2 = 3710 – subtrahend

Add the 1's complement of the subtrahend to the minuend now.

1 carry

$\frac{\begin{array}{r} 110101 \\ (+) 011010 \end{array}}{001111}$

1 carry

——————

0 1 0 0 0 0

Therefore, the solution is 010000. (010000)2 = 1610

Binary Subtraction Using 2's Complement

To implement this for subtracting two binary numbers, the very first step is to find the 2’s complement of the number which is to be subtracted from another number. To get the 2’s complement, first of all, 1's complement is found and then 1 is added to this. The addition is the required 2’s complement. Suppose, we need to find the 2’s complement of binary number 10010. First, find 1’s complement. To find this, replace all 1 to 0 and all 0 to 1. Therefore, 1’s complement of 10010 will be 01101. Now, add 1 to this as shown below.

To subtract a smaller number from a larger number using 2’s complement subtraction, the following steps are to be followed:

Step 1: Determine the 2’s complement of the smaller number

Step 2: Add this to the larger number.

Step 3: Omit the carry. Note that, there is always a carry in this case.

The following example illustrate the above-mentioned steps:

Exampe-1: Subtract (1010)2 from (1111)2 using 2’s complement method.

Solution:

Step 1: 2’s complement of (1010)2 is (0110)2.

Step 2: Add (0110)2 to (1111)2. This is shown below.

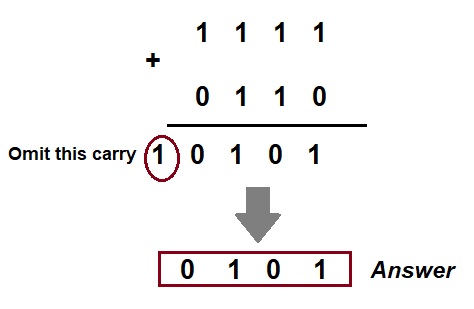
method of 2s complement subtraction of smaller number from a larger number

Subtraction of Larger Number from Smaller Number:

To subtract a larger number from a smaller number using 2’s complement subtraction, following steps are to be followed:

Step 1: Determine the 2’s complement of the larger number

Step 2: Add this to the smaller number.

Step 3: There is no carry in this case. The result is in 2’s complement form and is negative.

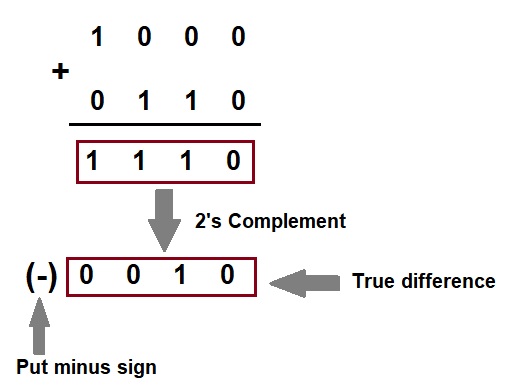
Step 4: To get answer in true form, take 2’s complement and change its sign.

Following example will definitely help you to understand the above steps

Example-2: Subtract (1010)2 from (1000)2 using 2’s complement.

Solution:

Step 1: Find the 2’s complement of (1010)2. It is (0110)2.

Step 2: Add (0110)2 to (1000)2.

steps for 2s complement subtraction of a larger number from smaller binary number

Step 3 and Step 4 has been explained in the above difference calculation.

You can use a great app that can help you with Number Systems and Boolean algebra, This app will give you all the answers to your question. Download the "Logic Kit" app on App Store to solve any problem in these subjects. Click here to download the app.